
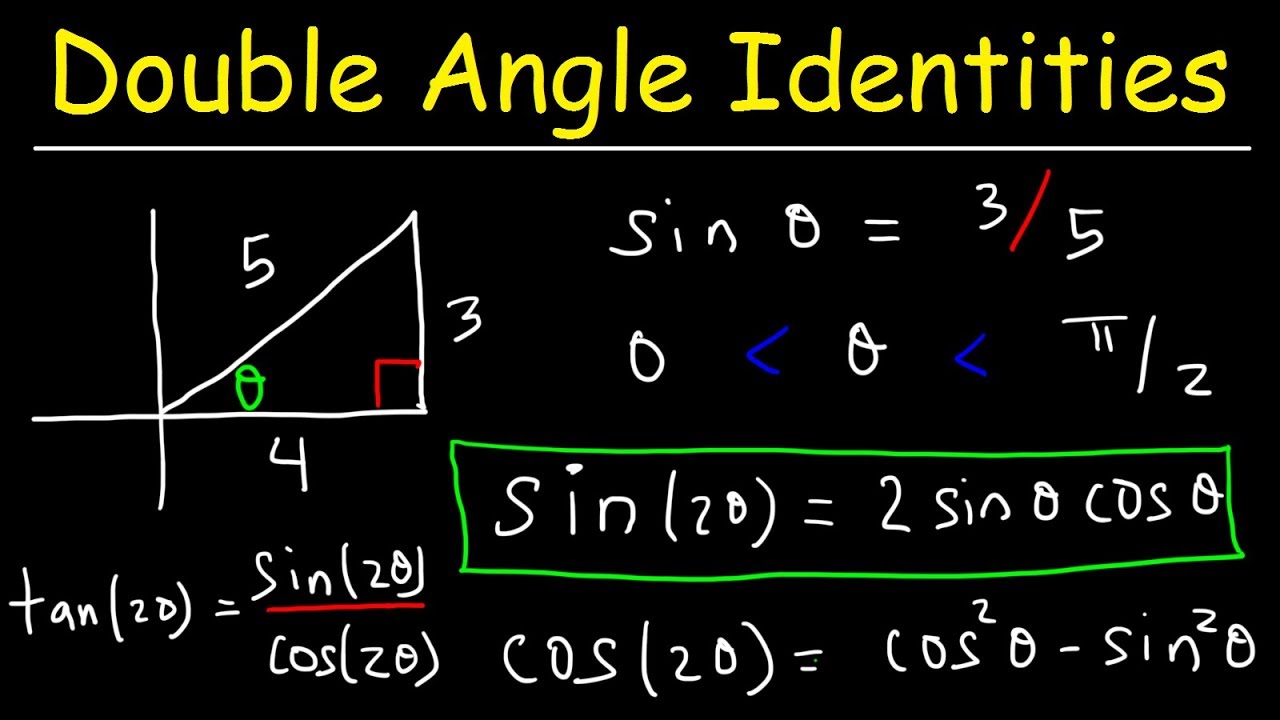
We can see that if we take the conditions for positive and negative values from #sinx# and #cosx# and divide them, we get that this is positive for quadrants I and III and negative for II and IV. We also notice that the trigonometric function on the RHS does not have a \(2\theta\) dependence, therefore we will need to use the double angle formulae to simplify \(\sin2\theta\) and \(\cos2\theta\) on the LHS. #color(blue)(tan(x/2) = pmsqrt((1-cos(x))/(1+cos(x))))# The right-hand side (RHS) of the identity cannot be simplified, so we simplify the left-hand side (LHS). Knowing how #cosx# is positive for and and negative for we know that it is positive for quadrants I and IV and negative for II and III. Knowing how #sinx# is positive for and negative for we know that it is positive for quadrants I and II and negative for III and IV.

We can derive them from the following identities: Now, prove the half-angle formula using the sine and cosine half-angle formulas.The half-angle identities are defined as follows: This method is exactly the same as the one above. If you did not prove these identities before, stop now and try to prove this one before moving ahead. In order to prove that , use the double-angle formula. In order to prove that , use the double-angle formula Thus in math as well as in physics, these formulae are useful to derive many important identities. Try using one of the identities that you learned in this module to derive these half-angle formulas.ĭid you try to derive the half-angle formulas yourself? Double angle identities and formula are useful for solving certain integration problems where a double formula may make things much simpler to solve. The rest of this section will cover methods of deriving these formulas, but try and do them yourself before moving ahead. The same is true for the half-angle formulas. All of these identities can be used to simplify more complex equations, and can be used to solve for angles using angles that you already know.Īs you have seen, you can use other identities to derive new ones. The more identities you know, the easier it will be for you to recognize the simplified solution to a complex expression. Yes, more identities! All of the identities we have learned, including the half-angle formulas, are still not the entirety of the trigonometric identities.

Half-angle formulas are more common than any other type of identity used in trigonometry.
QuestionĪnd from the standard points we learned above, we know that The method is the same as the one above.Ĭhallenge : Derive the cotangent, secant, and cosecant addition formulas that have not been given above. Use the sine and cosine addition formulas to prove that.
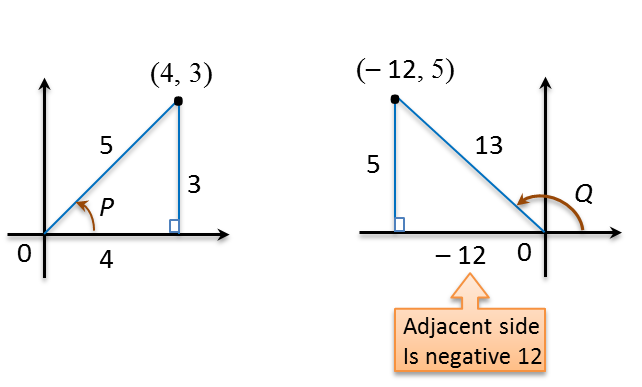
Using the addition formulas above, what is the formula for ? Pay close attention, because you will be asked to derive one of the addition formulas not given in this section at the end of this module. Using these sine and cosine formulas, you can easily derive the tangent, cotangent, secant, and cosecant addition formulas. Together, we will derive the formula for in order to get started in our effort to derive the other addition formulas. The sine and cosine addition formulas are: If you memorize these formulas, you can use information from the standard points you learned earlier to find uncommon points without using a calculator. The addition formulas are another group of identities that are useful tools for trigonometry. In an earlier section, we mentioned one of the addition formulas. There are six trigonometric ratios that can help you to solve for lengths of sides in right triangles. In this lesson, we will define and learn to apply addition, half-angle, and double-angle formulas. Half-Angle and Double-Angle Formulas Objective ⬅ Previous Lesson Workshop Index Next Lesson ➡


 0 kommentar(er)
0 kommentar(er)
